개요

반복되는 작업을 한 번만 할 수는 없을까? (재사용할 수 없을까?)

def fibonacci(n):
    if n == 1:
        return 1
    if n == 0:
        return 0
    else
        return fibonacci(n-1) + fibonacci(n-2)

print(fibonacci(10))

Q. 피보나치 수열을 구하는 위의 알고리즘을 생각해보자.
$n$번째 피보나치 수열의 값을 알아내지 위해 몇 번의 실행이 필요할까(시간복잡도는 어떻게 될까)?

$n$번째 피보나치 수열을 구하기 위해 필요한 작업의 수를 $T(n)$이라 하면 다음과 같은 점화식을 통해 작업의 수를 나타낼 수 있습니다.

\[\begin{align*} T(0) &= T(1) = 1 \\ T(n) &= T(n-1)+T(n-2) \\ T(n) &\approx 2^n \end{align*}\]

대략적으로, 호출 횟수를 트리로 나타내면 한 번의 호출당 자기 자신 두 번을 호출하고, 이 트리의 높이는 $n$이기 때문에 $2^n$의 호출이 일어났다고 볼 수 있습니다. 이는 매우 비효율적입니다.

하지만, 우리는 이 계산 과정에서 똑같은 문제가 계속해서 반복하여 계산된다는 생각을 할 수 있습니다. 이런 부분을 개선하여 더 빠른 연산을 할 수는 없을까요?

동적 계획법의 정의

동적 계획법(Dynamic Programming)
답을 구하기 위해 부분 문제의 답을 이용하여 효율적으로 정답을 계산하는 알고리즘 설계 기법

위의 피보나치 수열 문제에서 다시 생각해봅시다. fib(10)을 구하기 위해서는 fib(9), fib(8)의 값을 구해야 할 것입니다. 그리고 fib(9)의 값을 구하기 위해서는 fib(8), fib(7)의 값을 구해야 하고, fib(8)을 구하기 위해 fib(7), fib(6)의 값을 구해야 합니다. 여기서 우리는 fib(8)의 값을 구하는 작업이 반복된다는 것을 알 수 있습니다. 여기서, 일단 한번 구하고 값을 저장 후 재사용하면 더 빠르게 계산을 할 수 있을 것이라는 생각을 할 수 있습니다.

이 과정을 다음과 같이 구현할 수 있습니다.

memo = list(range(1000))

def fibonacci(n):
    if memo[n] != 0:
        return memo[n]
    if (n == 1):
        return 1
    if (n == 0):
        return 0
    else:
        memo[n] = fibonacci(n-1) + fibonacci(n-2)
        return memo[n]

print(fibonacci(10))

위와 같이 구현할 경우, 백트래킹에서의 경우와 비슷하게 트리를 그려보면, 한 번 구한 값에 대해서는 더 이상 함수를 호출하지 않으므로 연산 횟수가 줄어듭니다. 그리고 이는 다항식의 시간복잡도를 가집니다.
이런 구현 방법을 동적 계획법이라고 합니다.

최적 부분 구조 (Optimal Substructure)

최적 부분 구조
각 부분 문제의 답을 알 때, 전체 문제의 답을 쉽게 구할 수 있는 특성 - 문제의 특성을 의미

즉, 문제를 해결하는 과정에서 어떤 문제의 부분 문제의 해답으로 전체 문제를 해결할 수 있는 구조 자체를 최적 부분 구조라고 합니다. 다만, 최적 부분 구조는 어떤 문제의 특징일 뿐 문제를 푸는 과정은 아님에 명심합시다.

최적 부분 구조를 가진 다양한 예시를 살펴봅시다.

피보나치 수열 문제

피보나치 수열 문제에서도 최적 부분 구조를 확인할 수 있습니다.
$n$번째 피보나치 수를 구한다고 할 때, $n-1$번째, $n-2$번째 피보나치 수를 구하는 문제가 앞의 문제의 부분 문제가 됨을 알 수 있습니다. $\because f_n = f_{n-1}+f_{n-2}$

최단 거리 문제

다음의 지도를 함께 살펴봅시다. 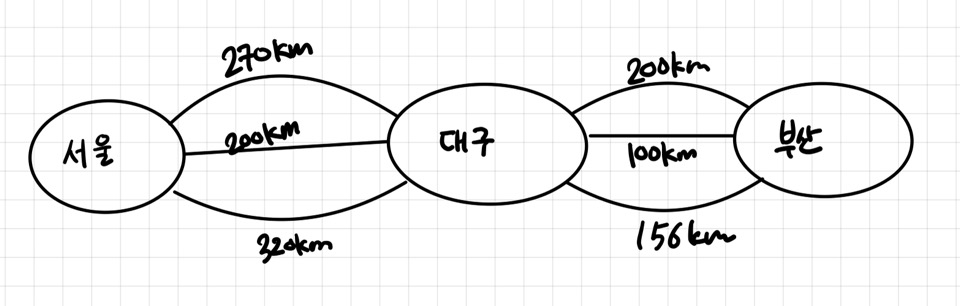alt text 위와 같이 서울에서 부산까지의 최단 경로를 구할 때, 대구를 무조건 거쳐야 하는 경우 이 문제를 다음과 같은 부분 문제로 나누어 생각할 수 있습니다.

서울 ~ 대구까지의 최단 경로 + 대구 ~ 부산까지의 최단 경로

이러한 구조도 역시 최적 부분 구조로 볼 수 있습니다.
다익스트라(Dijkstra) 알고리즘 등 최단 경로 알고리즘은 이러한 최적 부분 구조를 이용하는 문제입니다.

왜 최적 부분 구조가 중요하냐?

동적계획법에서도 보시다시피 최적 부분 구조를 이용해서 알고리즘의 문제 풀이 시간을 빠르게 하는 데에 유용하게 사용되는 구조이기 때문입니다.
동적계획법뿐만 아니라 분할 정복 알고리즘, 그리디 알고리즘에서도 최적 부분 구조가 유용하게 사용됩니다. 이러한 최적 부분 구조를 찾아 문제에 적용하는 것이 매우 중요합니다.

분할 정복 알고리즘과의 비교

분할 정복 알고리즘
문제를 부분문제로 분할하고 결합하는 과정을 통해 문제를 푸는 방법

분할 정복 알고리즘과 동적 계획법 두 방법에서 모두 문제의 최적 부분 구조를 찾아 문제를 풀이하는 특징을 갖습니다. 다만 다음의 요소에서 차이를 갖습니다.

  • 분할 정복은 보통 문제를 두 개 혹은 그 이상으로 나누고 각 문제를 한 번씩 해결합니다. (일반적으로 부분 문제를 풀며 얻은 답을 재사용하지 않습니다.)
  • 동적 계획법은 이미 이전에 구한 답을 저장하여 기존의 답을 최대한 활용하는 특징을 갖습니다.

Top-down과 Bottom-up 접근 방식

동적 계획법으로 문제를 푸는 방식에는 크게 두 가지 풀이 방법이 있습니다.

  • Top-down 접근법 : 큰 문제에서 작은 문제로 접근하는 방식
  • Bottom-up 접근법 : 작은 문제에서 큰 문제로 접근하는 방식

일반적으로, 두 가지 방법 모두 사용하여 DP 문제를 해결할 수 있습니다. 다만, 빨리 떠오르는 방식이 있고 두 가지 중 어떤 하나가 더 효율적인 경우 등 다양한 상황이 존재하기 때문에 두 가지 방법을 알고 적재적소에 이용하는 것이 중요합니다.

각각의 방식은 모두 점화식을 세우고 이를 구현하는 방식을 통해 구현하면 되는데, 문제 풀이의 방향만이 다르다고 생각할 수 있습니다.

일반적으로 Top-down 방식은 재귀함수를 통해 구현하고, Bottom-up 방식은 반복문을 이용하기 때문에 시간복잡도가 같더라도 Top-down 방식이 더 느릴 수 있습니다. 하지만, 일반적으로 Top-down 방식이 더 직관적입니다!

한편, python의 경우 재귀 호출 스택에 한계가 작게 설정되어 있기 때문에 다음 코드를 이용해 재귀 호출 스택을 늘려주어야 합니다. (파이썬은 기본적으로 재귀 호출 1000번만 가능하도록 설정되어 있음.)

import sys
limit_number = 100000 # 원하는 최대 재귀 호출 횟수
sys.setrecursionlimit(limit_number)

이제 다양한 예시 코드를 통해 두 방식을 구현하는 방법에 대해 더 자세히 알아봅시다!

Top-down 방식을 통한 피보나치 수열 함수 구현

다음과 같이 큰 문제와 작은 문제를 생각합시다.

  • 큰 문제: $n$번째 피보나치 수를 구하기
  • 작은 문제: $n-1$번째, $n-2$번째 피보나치 수를 구하기

그러면 다음과 같이 코드를 짤 수 있습니다.

def fibonacci(n):
    if (n == 1): # Basis Case
        return 1
    if (n == 0)
        return 0
    else:
        return fibonacci(n-1)+fibonacci(n-2) # Induction Case (점화식)

한편, 우리는 부분문제에서 구한 값을 재사용해야 하기 때문에 이를 저장해야 합니다. 이 과정을 우리는 메모이제이션(memoization)이라고 부릅니다. (메모리제이션이 아닙니다.)
메모이제이션을 이용한 코드는 아래와 같습니다.

memo = list(range(1000))

def fibonacci(n):
    if memo[n] != 0:
        return memo[n]
    if (n == 1):
        return 1
    if (n == 0):
        return 0
    else:
        memo[n] = fibonacci(n-1) + fibonacci(n-2)
        return memo[n]

Bottom-up 방식을 통한 피보나치 수열 구현

다음과 같이 큰 문제와 작은 문제를 생각합시다.

  • 큰 문제: $n$번째 피보나치 수를 구하기
  • 작은 문제: $n-1$번째, $n-2$번째 피보나치 수를 구하기

이 때, Bottom-up 방식에서는 가장 작은 문제부터 해결해야 하므로, $f_0, f_1$의 값부터 생각합시다. $f_0 = 1, f_1 = 1$인 점과 $f_n = f_{n-1} + f_{n-2}$인 점을 이용해 다음과 같은 반복문으로 구현합시다.

fibonacci = list(range(n+1))

# Basis case
fibonacci[0] = 0
fibonacci[1] = 1

# Induction case
for i in range(2, n+1):
    fibonacci[i] = fibonacci[i-1] + fibonacci[i-2]

print(fibonacci[n])

이 경우 자명하게 시간복잡도는 $O(n)$입니다.

동적 계획법을 이용한 문제 풀이

boj 1912 연속합

boj 1912 연속합 (S2)

  • 문제 설명
    • 입력: 자연수 $n$, $n$개의 정수로 이뤄진 수열
    • 출력: 연속된 수를 이용해서 구할 수 있는 부분합 중 가장 큰 값
  • 문제 풀이

먼저, 모든 경우에 대해 브루트포스를 진행할 시, $n$ 고려해야 하는 경우의 수는 $\binom{n}{2}$이므로 $O(n^2)$입니다. $n \le 100,000$이므로, 1초 안에 풀 수 없습니다.
따라서, 최적 부분 구조를 찾아서 동적 계획법을 이용해 문제를 풀어봅시다.
arr 배열에 입력된 배열을 저장하고, 길이가 같은 dp 배열을 새로 만듭니다. 그리고 dp[i]에는 i 번째 배열을 무조건 포함하면서 생각하는 배열의 길이를 하나씩 늘려 가며 생각한다고 해봅시다.
여기서 우리가 생각해야 하는 것은 dp[i]와 dp[i-1], 혹은 그 이전 값들과의 관계입니다. 여기서 우리는 다음과 같은 생각을 할 수 있습니다.

  • $\text{dp}[0] = \text{arr}[0]$
  • $\text{dp}[i-1]$이 양수일 때, $\text{dp}[i] = \text{arr}[i] + \text{dp}[i-1]$
  • $\text{dp}[i-1]$이 양수일 때, $\text{dp}[i] = \text{arr}[i] + 0$ $\because$ 음수를 더하는 것보다 $0$을 더하는 것이 이득!

따라서, 다음과 같은 점화식을 얻을 수 있습니다.

\[\text{dp}[i] = \text{max}(\text{dp}[i-1], 0) + \text{arr}[i]\]

이를 통해 모든 $0 \le i < n$에 대해서 0번째 원소부다 $i$번째 원소까지에 대해서 $i$번째 원소를 포함한 부분합에 대한 최댓값을 구할 수 있습니다. 최종적인 답은 $\text{dp}[0]$부터 $\text{dp}[n-1]$까지의 값 중 최댓값인 것을 자명하게 알 수 있습니다.

  • 예시 코드
#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using vll = vector<ll>;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    
    ll n;
    cin >> n;
    vll arr(n, 0), dp(n, 0);
    for (auto& k : arr) cin >> k;
    
    dp[0] = arr[0];
    for (ll i = 1; i < n; ++i) {
        dp[i] = max(dp[i-1], 0ll) + arr[i];
    }
    
    cout << *max_element(dp.begin(), dp.end());
}

boj 1463 1로 만들기

boj 1463 1로 만들기 (S3)

  • 문제 설명
  • 시간 제한: 0.15초
  • 다음 연산 세 가지만을 이용할 수 있을 때, 입력 값 $n~(1 \le n \le 10^6)$을 1로 만드는 연산 횟수의 최솟값을 구하여라.
    • $X$가 $3$으로 나누어떨어지면 $3$으로 나눈다.
    • $X$가 $2$로 나누어떨어지면 $2$로 나눈다.
    • $X$에 1을 뺀다.
  • 문제 풀이

위와 마찬가지로 Bottom-up 방식을 이용해서 문제를 풀어보겠습니다.
$\text{dp}[i]$를 $i$를 1로 만드는 최소 연산 횟수로 생각합시다.
그러면 다음과 같은 점화식을 얻을 수 있습니다.

\[\begin{align*} \text{dp}[1] &= 0 \\ \text{dp}[i] &= \begin{cases} \text{min}(\text{dp}[i-1], \text{dp}[i / 2]) + 1 & \text{if } i \equiv 0 \pmod 2 \cr \text{min}(\text{dp}[i-1], \text{dp}[i / 3]) + 1& \text{if } i \equiv 0 \pmod 3 \cr \text{dp}[i-1] + 1& \text{otherwise} \end{cases} \end{align*}\]
  • 예시 코드
#include <bits/stdc++.h>

using namespace std;

int main() {
    int n, cnt = 0;
    cin >> n;
    vector<int> d(n + 1, 0);
    for (int i = 2; i <= n; i++) {
        d[i] = d[i - 1] + 1;
        if (i % 2 == 0)
            d[i] = min(d[i], d[i / 2] + 1);
        if (i % 3 == 0)
            d[i] = min(d[i], d[i / 3] + 1);
    }

    cout << d[n];
}

boj 2293 동전 1

boj 2293 동전 1 (G5)

  • 문제 설명
  • 메모리 제한: 4MB

  • $n$가지 종류의 동전으로 $k$원을 만들고 싶을 때, 동전들로 $k$원을 만드는 경우의 수를 출력하는 문제

  • 문제 힌트

  • 각각의 동전의 개수에 대해서 동전을 추가할 때마다 경우의 수가 어떻게 바뀔지 생각해봅시다.

  • 문제 풀이

이 문제의 메모리 제한이 4MB임에 유의해야 합니다.

메모리 제한이 없을 경우 쉽게 생각할 수 있는 방법은 2차원 배열을 선언하여 문제를 푸는 것입니다.

$\text{dp}[i][j]$를 $0$~$i$번째 동전을 이용해 $j$원을 만드는 경우의 수로 생각해봅시다.
$\forall j,~ \text{dp}[0][j]=1$임이 자명합니다.

이제 $i$번째 동전에 대해 생각한다고 해봅시다. $i$번째 동전의 가치를 $k$원이라고 하면, $0 \le j < k$에 대해 $k$원 동전을 추가해서 어떤 경우도 만들 수 없으므로, $\text{dp}[i][j] = \text{dp}[i-1][j]$입니다.
한편, $j \geq k$의 경우, $j-k$원을 만드는 경우에 $k$원 동전을 추가하여 넣는 경우와 같으므로, 이 때의 점화식은 $\text{dp}[i][j] = \text{dp}[i-1][j] + \text{dp}[i][j-k]$과 같습니다.

메모리 제한이 없을 경우 이렇게 구현을 해도 상관 없겠지만, 우리는 단 4MB의 공간만이 존재합니다. 그렇기 때문에 공간을 줄이는 방법에 대해 생각해야 합니다.

여기서 2차원 배열을 사용하 필요가 없고 1차원 배열만으로 문제를 해결할 수 있다는 사실을 알 수 있습니다. 왜냐하면 문제를 푸는 과정 동안 모든 저장값이 필요하지 않고, 바로 직전 배열만이 필요하기 때문입니다. ($\text{dp}[i]$를 구할 때는 $\text{dp}[i-1]$만이 필요)

이를 줄이는 과정에 대한 설명은 아래 코드로 생략하겠습니다.

  • 에시 코드
// 2293 동전 1
#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using vll = vector<ll>;
using vvll = vector<vll>;

void solve();

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);

    solve();
}

void solve() {
    ll n, k;
    cin >> n >> k;

    vll v(n, 0);
    for (auto& k : v) {
        cin >> k;
    }

    vll dp(100'001, 0);
    dp[0] = 1;

    for (auto k_ : v) {
        for (int i = k_; i <= 100'000; i++) {
            dp[i] += dp[i - k_];
        }    
    }

    cout << dp[k];
}

boj 12865 평범한 배낭

boj 12865 평범한 배낭

  • 문제 설명

  • 각각 가치 $W$와 무게 $K$를 가지는 $N$개의 물건이 있을 때, 무게 $V$만큼 담을 수 있는 배낭에 넣을 수 있는 물건들의 최댓값을 구하시오.

  • 문제 풀이

먼저 어떻게 dp 배열을 설계해야 할지 생각해봅시다.
무게와 물건의 개수 둘 다 관여하므로 배열을 다음과 같이 짜봅시다.

dp[i][j]
i번째 물건까지 보았을 때, 가방 무게가 j 이하일 때 최대 가치

그러면 자연스럽게 정답은 $\text{dp}[N][K]$일 것입니다.

이제 점화식을 생각해봅시다. 편의상 이번에는 $1$번째 … $N$번째 문제로 생각해봅시다.

$\forall j~ \text{dp}[0][j]=0$임이 자명합니다. (아무것도 넣지 않은 상태 정의)
$i$번째 물건까지 봤고, 가방 무게가 $j$이하일 때의 최대 가치를 생각합시다.
$i$번째 물건을 포함시키지 않는 경우, $\text{dp}[i-1][j]$임이 자명합니다.
$i$번째 물건을 포함시키는 경우, $\text{dp}[i-1][j-w_i] + v_i$임이 자명합니다.

포함시킬 수 있는 경우에는 두 값 중 최댓값을, 그럴 수 없는 경우에는 $\text{dp}[i-1][j]$값을 넣으면 됩니다!

이러한 방식으로 푸는 문제를 흔히 배낭 문제라고 부릅니다.

  • 예시 코드
// 12865 평범한 배낭
#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using pll = pair<ll, ll>;
using vll = vector<ll>;
using vvll = vector<vll>;

struct dt {
    ll weight;
    ll value;
};

using vdt = vector<dt>;

int main() {
    ios::sync_with_stdio(false);
    cout.tie(0);
    cin.tie(0);

    ll i, j;
    ll n, k;
    cin >> n >> k;

    vdt g(n);
    vvll dp(n + 1, vll(k + 1, 0));

    for (auto &k : g) {
        ll a, b;
        cin >> a >> b;
        k = {a, b};
    }

    for (i = 0; i <= n; i++) {
        dp[i][0] = 0;
    }

    for (i = 1; i <= n; i++) {
        for (j = 0; j <= k; j++) {
            if (j >= g[i - 1].weight) {
                dp[i][j] = max(dp[i - 1][j], 
                dp[i - 1][j - g[i - 1].weight] + g[i - 1].value);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }

    cout << dp[n][k];
}

정리

  • 동적 계획법의 개념에 대해 학습했습니다.
  • 최적 부분 구조의 개념에 대해 학습했습니다.
  • Top-down 방식과 Bottom-up 방식에 대해서 학습하고, 각각의 구현 방법을 배웠습니다.
  • 다양한 dp 문제를 해결해보았습니다.

과제 문제

번호 문제번호 제목 난이도 분류
0 1003 피보나치 함수 S3 DP, 시간복잡도
1 1912 연속합 S2 DP
2 21463 1로 만들기 S3 DP
3 2293 동전 1 G5 DP
4 12865 평범한 배낭 G5 DP, 배낭 문제
5 2579 계단 오르기 S3 DP
6 11053 가장 긴 증가하는 부분 수열 S2 DP
7 11054 가장 긴 바이토닉 부분 수열 G4 DP
8 11055 가장 큰 증가하는 부분 수열 S2 DP
9 12852 1로 만들기 2 S1 DP, 최단거리 역추적
10 11726 2xn 타일링 S3 DP
11 11727 2xn 타일링 S3 DP
12 2133 타일 채우기 G4 DP, 챌린지
13 2294 동전 2 S4 DP, 챌린지
14 1750 서로소의 개수 S5 DP, 배낭 문제, 챌린지

다음시간 예고

  • 7주차
    • 그리디 알고리즘
    • 기초 정수론, 모듈로 연산, 빠른 팩토리얼, 조합 계산