[BOJ 1068] 트리

문제 링크

분류

그래프 탐색 (Graph Traversal), 깊이 우선 탐색 (Depth-first Search), 트리(Tree)

풀이

트리의 정의

트리는 그래프의 일종으로 다음의 조건을 갖는다.

무향의 그래프이다.
모든 노드(정점)가 연결되어 있다.
사이클(회로)가 존재하지 않는다.
이를 수학적 표시로 나타내면 다음과 같다.

\[\begin{align} & \quad \text{Given Graph } G=(V, E) \nonumber \\ \text{1.} & \quad \forall u, v \in V, (u, v) \in E \Rightarrow (v, u) \in E \nonumber \\ \text{2.} & \quad \exists u,v \in V \text{ such that there exists a path from } u \text{ to } v \text{ in } G \nonumber \\ \text{3.} & \quad \forall \text{ distinct vertices } u,v \in V, \exists \text{ at most one path from } u \text{ to } v \text{ in } G \nonumber \end{align}\]

루트, 부모, 자식

이 트리에서 루트를 정의하면 자식-부모 관계를 정의할 수 있다.
루트는 트리에서 가장 높은 곳에 위치하는 노드를 의미한다.
부모는 트리를 구성하는 임의의 노드의 한 단계 상위 노드를 의미하며, 자식은 트리를 구성하는 임의의 노드의 한 단계 하위 노드를 의미한다.

[예시 그림] 트리 예시 그림

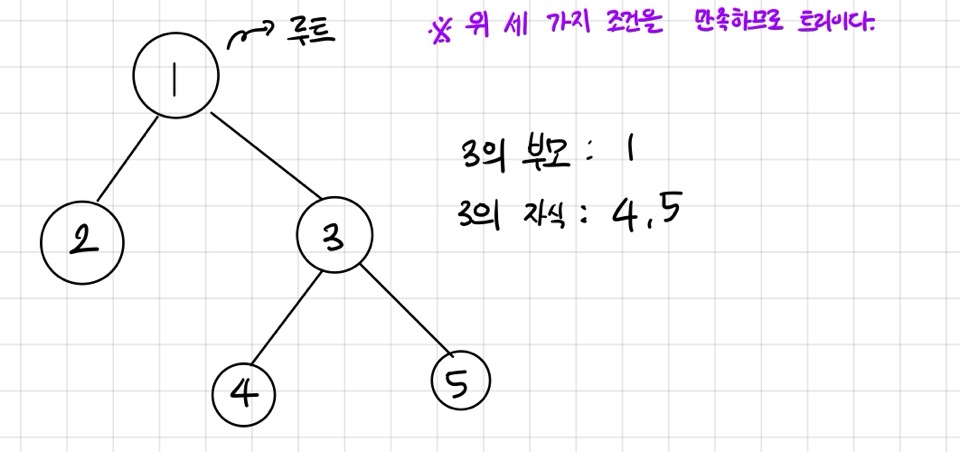
문제 해석 및 문제 풀이

문제에서는 임의의 트리를 입력 받고 어떤 노드를 하나 지웠을 때 리프 노드, 즉 자식이 없는 노드의 개수를 구하는 것이 문제이다.
이를 구하기 위해 먼저 지우려는 노드가 없을 때 리프 노드의 개수를 구하는 방법을 살펴보자. 루트에서 자식으로의 깊이 우선 탐색을 진행하고, 각각의 깊이 우선 탐색 과정에서 자식의 개수를 셈으로써 자식 노드가 없는 노드를 찾을 수 있다.
한편, 노드를 지우게 될 경우 위의 경우에서와 달리 지운 노드 하위의 그래프는 고려하여서는 안 되므로 재귀함수로 구현된 DFS에서 빠르게 함수를 반환하는 방법을 이용할 수 있다.
여기서 주의해야 하는 점은 루트가 지워졌을 때인데, 구현된 코드에서 루트와 지우려는 노드가 똑같은 경우 지우는 노드가 없는 경우가 계산되는 문제점이 존재했다. 그렇기 때문에 루트와 지우려는 노드가 다를 때에만 깊이 우선 탐색을 진행하여야 한다.

코드

깃허브 코드 링크

// 1068 트리
#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using vll = vector<ll>;
using vvll = vector<vll>;

vll visited;
vvll g;
ll ans;

void dfs(ll x, ll del) {
    if (visited[x] == 1) return;

    visited[x] = 1;
    if (g[x].empty()) {
        ans++;
        return;
    }
    if (g[x].size() == 1 && g[x][0] == del) {
        ans++;
        return;
    }

    for (auto k : g[x]) {
        if (k != del) {
            dfs(k, del);
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    ll n;
    cin >> n;

    g.resize(n, vll(0));
    visited.resize(n, 0);

    ll i, j, tmp, root;
    for (i = 0; i < n; i++) {
        cin >> tmp;
        if (tmp == -1) {
            root = i;
            continue;
        }
        g[tmp].push_back(i);
    }

    ll del;
    cin >> del;
    
    if (root != del)
        dfs(root, del);
    cout << ans;
}